When it comes to FEA, material response under different loading conditions is calculated using mathematical models. These tools help us predict how an object will respond to a specific load, and this knowledge is crucial for designing safe and efficient structures and products. One such mathematical model is the Johnson-Cook material model.
Developed by W. Johnson and R. Cook in the 1980s, the Johnson-Cook material model is a constitutive model that describes the behavior of metals under large strains and high strain rates.[1] It’s a phenomenological model based on experimental data, and it’s widely used in finite element analysis (FEA) simulations.
It’s worth noting that the Johnson-Cook model is not suitable for all materials or loading conditions. It’s primarily designed for metal materials under high strain-rate loading conditions, so it may not be appropriate to use this model in situations where the loading conditions are not high strain-rate or where the material being modeled is not a metal.
But what exactly is this model and how does it work? The Johnson-Cook material model is represented by equation (1), which takes into account the strain rate, temperature, and the plastic deformation of the material.
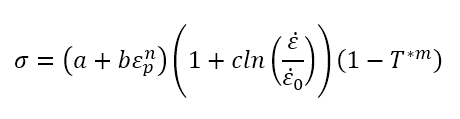
The equation is composed of three different terms, each representing the influence of a specific factor on the material’s behavior. The first term of the equation represents the influence of plastic strain on the material. Plastic strain is the amount of deformation that a material experiences when it is loaded beyond its elastic limit. The second term of the equation represents the influence of strain rate on the material. Strain rate is the rate at which a material is deformed. This term accounts for the fact that materials behave differently at high strain rates compared to low strain rates. The third term of the equation represents the influence of temperature change on the material. Temperature changes can affect the properties of a material, such as its strength and ductility.
σ-Flow stress:
Flow stress is the internal stress that develops within a material when it is deformed. In the context of the Johnson-Cook material model, flow stress is the stress that is required to maintain a certain level of deformation in a metal material under high strain-rate loading conditions [2].
εp– Plastic strain:
Plastic strain is the permanent deformation of a material that occurs when it is loaded beyond its elastic limit.
As shown in Figure 1, when a material is loaded, it will first experience elastic deformation, which is reversible and disappears when the load is removed. But when the load exceeds the elastic limit, the deformation becomes permanent and is known as plastic deformation. The amount of plastic deformation that a material experiences is referred to as plastic strain.
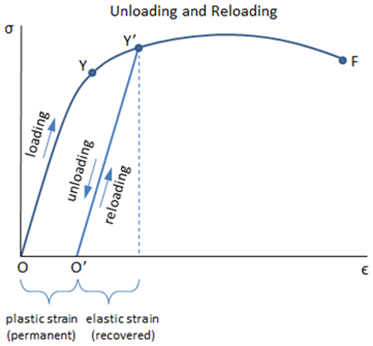
a-Yield stress:
Yield stress is the limit of elastic deformation of a material, and the point at which it begins to deform permanently. It’s an important value for engineers and designers to know. The yield stress can be influenced by several factors such as temperature, strain rate, and the microstructure of the material, so it’s important to consider these factors when determining the yield stress of a material.
b-Hardening modulus (Hardening parameter):
The hardening modulus is a measure of how much the flow stress of a material increases as it is loaded beyond its yield point. It is often represented as the slope of the stress-strain curve between the yield point and the ultimate tensile strength point [4]. A material with a high hardening modulus will have a steeper slope on the stress-strain curve, indicating that its flow stress increases rapidly as it is loaded beyond its yield point. A material with a low hardening modulus will have a flatter slope on the stress-strain curve, indicating that its flow stress increases more slowly as it is loaded beyond its yield point.
n-Hardening exponent:
The hardening exponent shows how stress varies between the yield point and ultimate tensile strength point with respect to strain in a stress-strain curve.
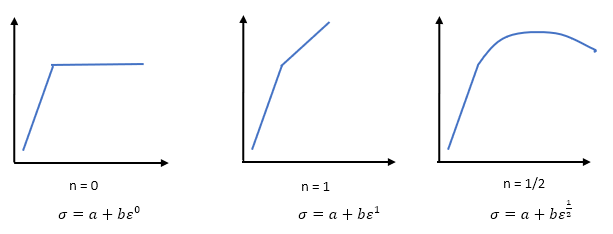
ε – Strain rate:
The strain rate is a measure of the rate at which the strain changes over time. In other words, it is the rate at which a material is deformed under an applied load. The strain rate can have a significant effect on the stress-strain curve of a material
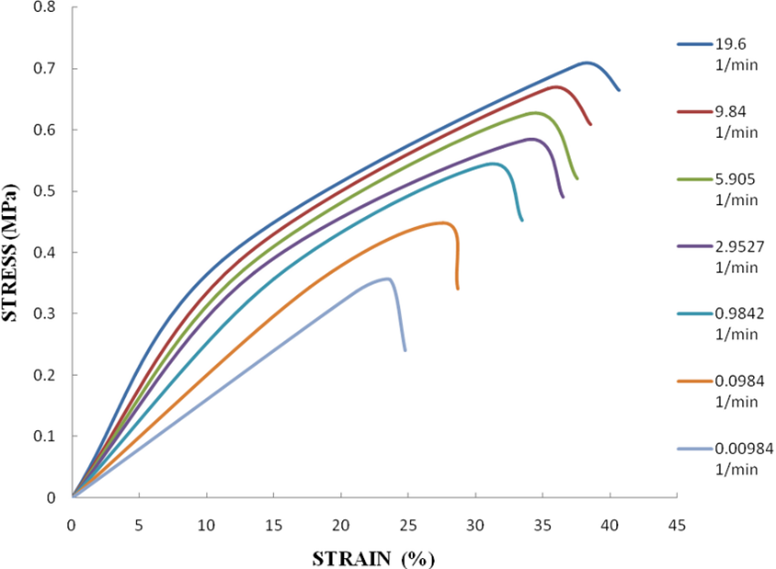
ε0 – Reference strain rate:
Reference strain rate is a commonly used standard for comparing the sensitivity of different materials to strain rate. It is typically measured in units of s-1.
c-Strain rate coefficient:
Strain rate coefficient represents the amount of change in flow stress for a unit change in strain rate at a specific plastic strain.
m-Temperature exponent
This measures the sensitivity of the material to temperature.
T*-Temperature
Applications and Limitations
The Johnson-Cook material model can be used to simulate the behavior of metal structures under extreme conditions, such as high-temperature and high-pressure environments. Some examples of applications of the Johnson-Cook material model include:
- Modeling the response of armor plates to impact from projectiles
- Predicting the response of metal structures in nuclear power plants to extreme loading events such as earthquakes and pressure pulses
- Analyzing the behavior of metal components in automotive and transportation systems during crash events
- Investigating the deformation and failure of metal structures in industrial and manufacturing processes, such as stamping and forging.
It’s also worth noting that the Johnson-Cook model is a phenomenological model that is based on experimental data, which means that it may not accurately represent the behavior of a material in all cases and under all loading conditions. Therefore, it is important to validate the model against experimental data before using it for a specific application. Some examples of when the Johnson-Cook model should not be used include:
- Modeling the behavior of materials that are not metals, such as ceramics, polymers, or composites, as the model is not formulated for these types of materials.
- Modeling the behavior of materials at high temperatures and low strain rates, as the model is not formulated to consider the thermal effects on material properties under low strain-rate conditions.
Conclusion
In conclusion, the Johnson-Cook material model is a powerful tool for understanding the behavior of metals under high strain-rate loading conditions. Its wide use in FEA simulations makes it an essential tool for engineers and designers working with metal structures. However, it’s important to validate the model against experimental data before using it for a specific application and to ensure it’s appropriate for the material and loading conditions being considered.
References
[1] A. Hallén and J. Hjorth, “Development of Methodology for Finite Element Simulation of Overhead Guard Impact Test,” Dissertation, 2022.
[2] “Johnson-Cook Plasticity Model (LAW2),” 2022.help.altair.com. https://2022.help.altair.com/2022.1/hwsolvers/rad/topics/solvers/rad/theory_material_laws_elastic_plastic_isotropic_materials_jc_plas_model_r.htm#theory_9_3_1.
[3] MechaniCalc, “Mechanical Properties of Materials | MechaniCalc,” Mechanicalc.com, 2011. https://mechanicalc.com/reference/mechanical-properties-of-materials
[4] “The influence of Johnson-Cook parameters on Stress-strain graph and their requirements.,” www.youtube.com. https://www.youtube.com/watch?v=LV-ooT0dg7k (accessed Jan. 14, 2023).
[5] W. M. Adel, H. Kamal, and D. El-Soualey, “Experimental Determination of Some Design Properties of Viscoelastic Solid Propellant Using Uniaxial Tensile Test,” May 2011. [Online]. Available: https://www.researchgate.net/publication/305280086_Experimental_Determination_of_Some_Design_Properties_of_Viscoelastic_Solid_Propellant_Using_Uniaxial_Tensile_Test
