Introduction
Partial differential equations (PDEs) are most commonly employed for solving complex problems in engineering. However, solving PDEs analytically is hard and obtaining exact solution is almost impossible. Therefore, when solving PDEs, we use discrete numerical methods which provide an approximation to the real solution. Finite Element Method (FEM) is one method used to approximate a solution. This method divides a system into a finite number of small elements, solving simplified equations for each element to obtain a solution for the system.
The equations in FEA are simplified by applying infinitesimal displacements and rotations to the finite elements. This method delivers accurate solutions for systems subjected to small deformations but is not very effective for systems undergoing large deformations. Solving complex systems subjected to large deformations needs a more sophisticated method. This is where the Large Deformation Theory comes into play.
Large Deformation Theory
For the case of large displacements and large strains, deviation from the small deformation theory is needed. This deviation is obtained by constructing a co-rotational, updated Lagrangian formulation using the rate of deformation tensor [1].
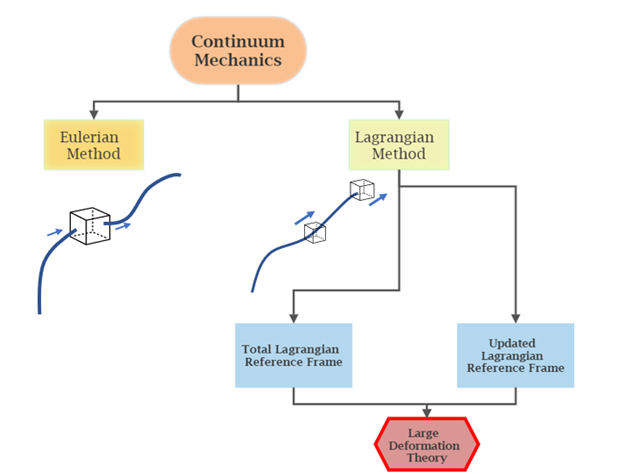
Formulation of co-rotational updated Lagrangian is based on the basic reference frames which are used in continuum mechanics.
- Eulerian reference frame 🡪 fundamentally used to solve fluid mechanics problems which use a fixed area and study the particles which are traveling through the area.
- Lagrangian reference frame 🡪 fundamentally used to solve solid mechanics problems. This can be divided into main two parts considering the changes in coordinate systems that are used in each method.
- Total Lagrangian reference frame 🡪 Here the particles are analyzed considering a fixed initial reference coordinate system.
- Updated Lagrangian reference frame 🡪 Here the analysis of the particles is done by relating the current coordinate system to the previous current coordinate system of the particles. Therefore, in this method, the time step is considered fixed, and the reference frame moves with the particle.
The co-rotational Lagrangian formulation is achieved by further developing the previous types of Lagrangian methods. Measurements for rigid body rotations and translations are taken with respect to a fixed reference frame, and measurements for deformations are taken with respect to each element’s own coordinate system. The position of each element’s coordinate system is varying with the motion of the rigid body which directs to a co-rotation with the rigid body.
For further information on the formulation of Large Deformation The formulation of theory can be discovered by referring to references 1 and 2.
Summary
When solving a complex geometrical problem, infinitesimal displacements (strains) and rotations are considered. From rotations and the displacements, rotations are the most critical property which leads to violation of small deformation theory. If we consider a system which is subjected to quite big rotations and analyze the system, small deformation theory is not applicable because the elements of linear strain tensor can be non-zero even if there is no deformation in the system
To compare the limitations of applicability of large deformation theory in different systems, each system can be considered as one of the following kinematic conditions. According to the relevant kinematic condition, the problem can be solved by using either small or large deformation theories.
- Small displacements and small strain conditions – small deformation theory can be used
- Large displacement and rotation with small strains – total Lagrangian reference frame can be used
- Large displacements and large strains – either total or updated Lagrangian reference frame can be used
To solve problems undergoing large deformations using FEA, deviation from basic theorems of FEM is needed. As mentioned above, that deviation is obtained through the Large Deformation Theory.
References
[1] K.-J. Bathe, Finite Element Procedures, Upper Saddle River, New Jersy: Prentice-Hall Inc., 1996.
[2] A. H. &. J. Hjorth, Development of Methodology for Finite Element Simulation of Overhead Guard Impact Test, Link¨oping: LiU Electronic Press, 2022.
